The Stone-Weierstraß theorem

( Part of the ‘23 lecture Building Blocks of Modern Machine Learning: (Self-)Attention and Diffusion Models. )

Theorem 1 (Stone-Weierstraß)

Let \(K \subset \mathbb R^d\) be a compact set. Consider the \(\mathbb R\)-algebra \(C(K,\mathbb R)\) of continuous, real-valued functions on it. Let \(\mathcal A \subset C(K,\mathbb R)\) be a subalgebra, satisfying

1. \(\mathcal A\) contains the constant function \(1\).

2. \(\mathcal A\) separates points, that is, for every \(x,y \in K\), \(x\not= y\) there exists \(\phi \in \mathcal A\) such that

\[ \phi(x) \not= \phi(y).\]

Then: \(\mathcal A\) is dense in \(C(K,\mathbb R)\) with respect to the supremum norm

\[ ||f||_\infty := \sup_{z\in K} |f(z)|.\]

That is, for every \(f \in C(K,\mathbb R)\), every \(\epsilon > 0\) there exists a \(g \in \mathcal A\) such that

\[ ||f-g||_\infty < \epsilon.\]

We will follow the beautiful proof of [BD81]. A key ingredient is the following inequality.

Lemma 1 (Bernoulli’s inequality)

For \(z \ge -1\) and \(m \in \mathbb N_{\ge 1}\), we have

\[ (1+z)^m \ge 1 + mz.\]

Proof

For \(z \ge 0\) the inequality follows from

\[ (1+z)^m = \sum_{k=0}^m \binom{m}{k} z^k = 1 + mz + \text{ non-negative terms }.\]

For \(z=-1\) the inequality reads as

\[ 0 \ge 1 - m,\]

which is true for \(m \ge 1\). To prove the inequality on \([-1,0]\) it is now sufficient to show that the derivative of

\[ (1+z)^m - 1 - mz,\]

does not change sign on \([-1,0]\). And, indeed

\[ \frac{d}{dz} \dots = m (1+z)^{m-1} - m \le 0 \quad z \in [-1,0]. \]

Using this lemma we can show that, on \([0,1]\), we can approximate a certain step-function arbitrarily close by a polynomial.

Lemma 2

Given \(\delta \in (0,1)\), \(\epsilon > 0\), there exists a polynomial \(\Phi\) in one variable such that

1. \(\Phi(y) \in [0,1]\) for \(y \in [0,1]\).

2. \(\Phi(y) \in [1-\epsilon,1]\) for \(y \in [0,\frac\delta2]\).

3. \(\Phi(y) \in [0,\epsilon]\) for \(y \in [\delta,1]\).

Proof

Pick \(k \in \mathbb N_{\ge 1}\) such that

\[ 1 < k\delta < 2.\]

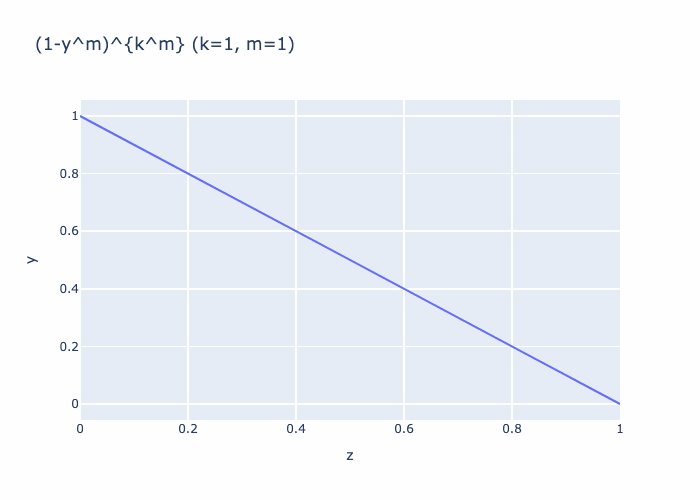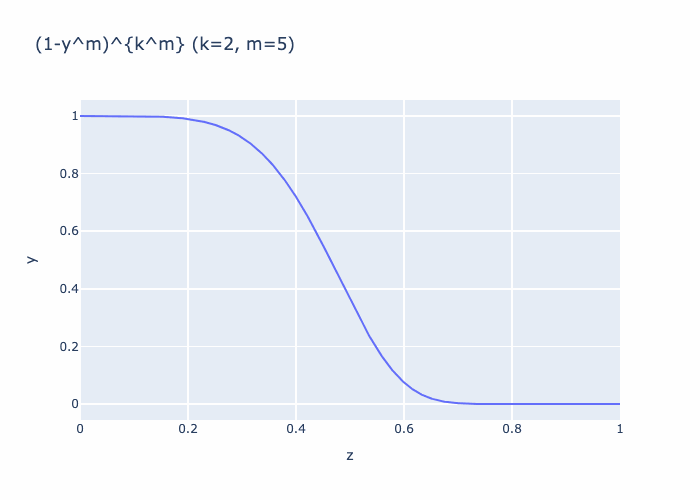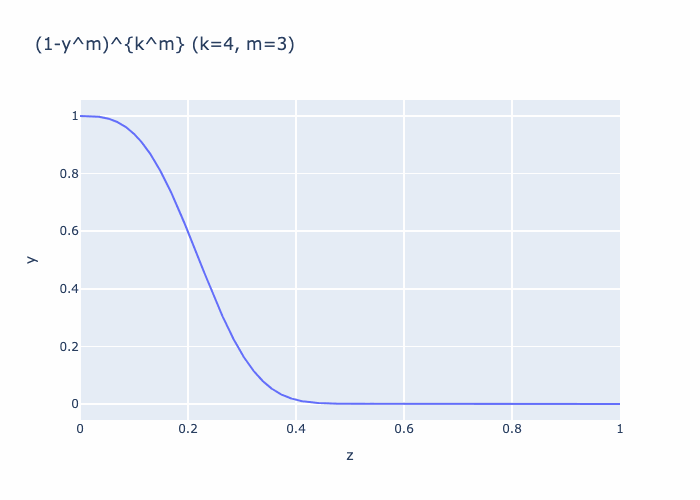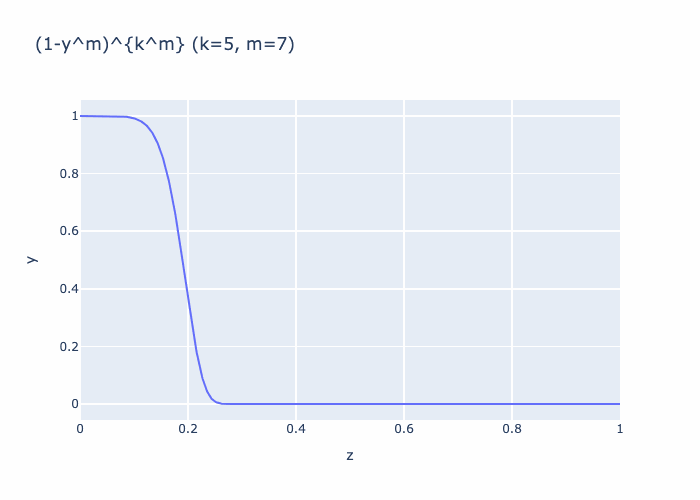
Given \(m \in \mathbb N_{\ge 1}\) define

\[ \Phi_m(y) := (1-y^m)^{k^m}.\]

Then

\[ \Phi_m(y) \in [0,1] \quad \forall y \in [0,1].\]

Further, for \(y \in [0,\frac\delta2]\) and using Bernoulli’s inequality

\[ \Phi_m(y) \ge 1 - k^m x^m > 1 - \left(\frac{k\delta}2\right)^m.\]

We observe that since \(k\delta/2 < 1\), this tends to \(1\) (independent of \(y \in [0,\frac\delta2]\)).

For \(y \in [\delta,1]\)

\[\begin{align*} \Phi_m(y) &= \frac{1}{k^m x^m} (1-y^m)^{k^m} k^m x^m \\ &\le \frac{1}{k^m x^m} (1-y^m)^{k^m} (1 + k^m x^m) \\ &= \frac{1}{k^m x^m} (1-y^{2m})^{k^m} \\ &\le \frac{1}{k^m x^m} \\ &\le \frac{1}{(k\delta)^m} \\ \end{align*}\]

Here we used Bernoulli’s inequality for the second line. We observe that since \(k\delta > 1\), this tends to \(0\) (independent of \(y \in [\delta,1]\)).

Together, we see that we can choose \(m\) large enough such that \(\Phi := \Phi_m\) satisfies the required bounds.

Lemma 3

Under the assumptions of the theorem, for every point \(x_0 \in K\), every open neighborhood \(U \subset K\) of \(x_0\) there is a smaller neighborhood \(U' \subset U\) of \(x_0\) such that for every \(\epsilon > 0\) there is a \(\phi \in \mathcal A\) with

\[\begin{align*} 0 \le \phi &\le 1 \\ \sup_{z \in U'} |1 - \phi(z)| &< \epsilon \\ \sup_{z \in K \setminus U} |0 - \phi(z)| &< \epsilon. \end{align*}\]

Proof

For every \(x \in K\) there is \(\psi_x \in \mathcal A\) with

\[\begin{align*} \psi_x(x) \not= \psi_x(x_0). \end{align*}\]

Define \(\psi_x' := \psi_x - \psi_x(x_0) \in \mathcal A\). Then

\[\begin{align*} \psi'_x(x) \not= 0 = \psi'_x(x_0). \end{align*}\]

Define

\[\begin{align*} \psi''_x := \frac{1}{||\psi_x'||^2} (\psi'_x)^2. \end{align*}\]

Then

\[\begin{align*} &0 \le \psi''_x \le 1 \\ &\psi''_x(x_0) = 0\\ &\psi''_x(x) > 0. \end{align*}\]

Define

\[\begin{align*} V_x := \{ z \in K : \psi''_x(z) > 0 \}. \end{align*}\]

Then \(V_x\) is an open neighborhood of \(x\). Hence

\[\begin{align*} \bigcap_{x\in K\setminus U} V_x \supset K\setminus U. \end{align*}\]

Seince \(K\setminus U\) is compact, there exists a finite family of points \(x_1, \dots, x_n \in K\) with

\[\begin{align*} \bigcap_{i=1}^n V_{x_i} \supset K\setminus U. \end{align*}\]

Define

\[\begin{align*} p := \frac1n \sum_{i=1}^n \psi''_{x_i}. \end{align*}\]

Then

\[\begin{align*} &0 \le p \le 1 \\ &p(x_0) = 0\\ &p(y) > 0 \qquad y \in K\setminus U. \end{align*}\]

Define

\[\begin{align*} &0 \le p \le 1 \\ &p(x_0) = 0\\ &p(y) > 0 \qquad y \in K\setminus U. \end{align*}\]

By compactness of \(K\setminus U\) there is a \(\delta > 0\) such that

\[\begin{align*} p(y) > \delta \qquad y \in K\setminus U. \end{align*}\]

Define

\[\begin{align*} U' := \{ y \in K : p(y) < \delta/2 \}. \end{align*}\]

Then \(U' \subset U\) and

\[\begin{align*} &0 \le p(y) < \delta/2 \text{ on } U' \\ &\delta \le p(y) \le 1 \text{ on } K\setminus U. \end{align*}\]

Using Lemma 2, there is a Polynomial \(\Phi\) such that

\[\begin{align*} \Phi(p) & \in [0,1] \text{ on } K \\ \Phi(p) &\in [1-\epsilon,1] \text{ on } U' \\ \Phi(p) &\in [0,\epsilon] \text{ on } K\setminus U. \end{align*}\]

Hence, \(\phi := \Phi(p) \in \mathcal A\) does the job.

We can now prove the theorem.

Proof of Stone-Weierstraß.

Claim: for all closed subsets \(A,B \subset K\), \(A \cap B = \emptyset\), for every \(0< \epsilon <1\) there is \(\phi \in \mathcal A\) such that

\[\begin{align*} 0 &\le \phi \le 1 \\ 0 &\le \phi < \epsilon, \text{ on } A \\ 1-\epsilon &\le \phi \le 1, \text{ on } B. \end{align*}\]

Indeed, let \(U := K \setminus B\). For \(x \in A\) consider the neighborhood \(U' = U'_x\) of \(x\) (Lemma 3). Since \(A\) is compact, there exist \(x_1, \dots, x_m \in A\) such that

\[\begin{align*} A \subset \bigcup_{i=1}^m U'_{x_i}. \end{align*}\]

By the choice of \(U'_{x_i}\) ther exists \(\phi_i \in \mathcal A\) such that

\[\begin{align*} 0 \le \phi_i &\le 1 \\ \sup_{z \in U'_{x_i}} |1 - \phi_i(z)| &< \epsilon/m \\ \sup_{z \in K \setminus U'_{x_i}} |0 - \phi_i(z)| &< \epsilon/m. \end{align*}\]

Define

\[\begin{align*} \phi := (1-\phi_1) \cdot \dots \cdot (1-\phi_m). \end{align*}\]

Then

\[\begin{align*} &0 \le \phi \le 1 && \\ &0 \le \phi < \epsilon / m < \epsilon && \text{ on } \bigcup_{i=1}^m U'_{x_i} \supset A \\ &1-\epsilon \le (1-\epsilon/m)^m \le \phi \le 1 && \text{ on } B. \end{align*}\]

This proves the claim.

Let now \(f \in C(K,\mathbb R)\) be given. By considering \(f + ||f||_\infty\) we can assume that \(f \ge 0\). Let \(0 < \epsilon < 1/3\) be given. Choose \(n \in \mathbb N_{\ge 1}\) with

\[\begin{align*} (n-1) \epsilon \ge ||f||_\infty. \end{align*}\]

Define for \(j=0,\dots,n\)

\[\begin{align*} A_j &:= \left\{ x \in K : f(x) \le (j-\frac13) \epsilon \right\} \\ B_j &:= \left\{ x \in K : f(x) \ge (j+\frac13) \epsilon \right\}. \end{align*}\]

Then

\[\begin{align*} \emptyset = A_0 &\subset A_1 \subset \dots \subset A_n = K \\ B_0 &\supset B_1 \supset \dots \supset B_n = \emptyset. \end{align*}\]

Using the claim, we can take \(\phi_i \in \mathcal A\) with

\[\begin{align*} 0 &\le \phi_i \le 1 && \\ 0 &\le \phi_i < \epsilon / n && \text{ on } A_j \\ 1-\epsilon/n &\le \phi_i \le 1 && \text{ on } B_j. \end{align*}\]

Set

\[\begin{align*} g := \epsilon \sum_{i=0}^n \phi_i. \end{align*}\]

For \(x \in K\) there exists a \(j \in \mathbb N_{\ge 1}\) such that

\[\begin{align*} x \in A_j \setminus A_{j-1}. \end{align*}\]

In particular

\[\begin{align*} (j-\frac43)\epsilon < f(x) \le (j-\frac13) \epsilon, \end{align*}\]

and

\[\begin{align*} \phi_i(x) < \epsilon/n \text{ for every } i \ge j. \end{align*}\]

Moreover, \(x \in B_i\) for every \(i \ge j-2\) which implies

\[\begin{align*} \phi_i(x) > 1 - \epsilon/n \text{ for every } i \le j-2. \end{align*}\]

Then

\[\begin{align*} g(x) = \epsilon \sum_{i=0}^n \phi_i(x) = \epsilon \sum_{i=0}^{j-1} \phi_i(x) + \epsilon \sum_{i=j}^{n} \phi_i(x) \le j \epsilon + \epsilon (n-j+1) \frac\epsilon{n} \le j\epsilon + \epsilon^2 < (j+\frac13) \epsilon. \end{align*}\]

If \(j \ge 2\), then

\[\begin{align*} g(x) &\ge \epsilon \sum_{i=0}^{j-2} \phi_i(x) \ge (j-1) \epsilon (1-\epsilon/n) = (j-1) \epsilon (1-\epsilon/n) - (j-1) \epsilon^2 / n \\ &> (j-1) \epsilon - \epsilon^2 > (j-\frac43) \epsilon. \end{align*}\]

If \(j=1\), then

\[\begin{align*} g(x) > (j-\frac43) \epsilon, \end{align*}\]

is trivially true. Hence

\[\begin{align*} |f(x)-g(x)| < (j+\frac13)\epsilon - (j-\frac43)\epsilon < 2 \epsilon, \end{align*}\]

as desired.

[BD81]

Bruno Brosowski and Frank Deutsch. An elementary proof of the stone-weierstrass theorem. Proceedings of the American Mathematical Society, 81(1):89–92, 1981.